另外,他们还有两条性质
1、函数的和的不定积分等于各个函数的不定积分的和;即:设函数f(x)及 g(x)的原函数存在,则
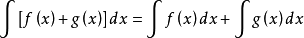
2、求不定积分时,被积函数中的常数因子可以提到积分号外面来。即:设函数
的原函数存在,
为非零常数,则

学霸君:好,辛苦你了∫e^(-x^2)不定积分,你先下去吧。
小e:老哥,对方看起来确实很厉害啊,接下来该怎么办?

学霸君:别着急,我之前已经了解过了,不定积分军基本上都是以这十三种为基础的


学霸君:除此之外,我已经找到了几种对付他们的方法。
小e:哦,都有什么方法?

学霸君:老弟请看,主要有三大方法,分别为第一类换元法(即凑微分法),第二类换元法,还有分部积分法。
小e:哦,凑微分法我听说过,据说是通过凑微分,最后依托于某个积分公式,进而求得原不定积分,常用的有这几种:





学霸君:对的,没错,那就是第一类换元法,就是把微分凑成可以变到d后面的形式,接下来我们看第二类换元法,第二类换元法化简不定积分的关键仍然是选择适当的变换公式 x = φ(t)。此方法主要是求无理函数(带有根号的函数)的不定积分。由于含有根式的积分比较困难,因此我们设法作代换消去根式,使之变成容易计算的积分。
下面我简单介绍第二类换元法中常用的方法:
(1)根式代换:被积函数中带有根式√(ax+b),可直接令 t =√(ax+b);
(2)三角代换:利用三角函数代换,变根式积分为有理函数积分,有三种类型:
被积函数含根式√(a^2-x^2),令 x = asint
被积函数含根式√(a^2+x^2),令 x = atant

被积函数含根式√(x^2-a^2),令 x = asect
注:记住三角形示意图可为变量还原提供方便。
(3)倒代换(即令 x = 1/t):设m,n 分别为被积函数的分子、分母关于x 的最高次数,当 n-m>1时,用倒代换可望成功;
(4)指数代换:适用于被积函数由指数 a^x 所构成的代数式;
(5)万能代换(半角代换):被积函数是三角函数有理式,可令 t = tan(x/2)
小e:哦,对了,我曾听别人说过,在三角代换中
可以用一个三角形让计算简单一些。

学霸君:之后就是最后一种方法了,也就是
当被积函数是两种不同类型函数的乘积时,用分部积分法

设函数和u,v具有连续导数,则d(uv)=udv+vdu。移项得到udv=d(uv)-vdu两边积分,得分部积分公式∫udv=uv-∫vdu。①。称公式①为分部积分公式.
如果积分∫vdu易于求出,则左端积分式随之得到.分部积分公式运用成败的关键是恰当地选择u,v
一般来说,u,v选取的原则是:
1、积分容易者选为v,
2、求导简单者选为u。
除此之外,还有一句口诀,反对幂指三,前u后dv。
小e:哇!!!不愧为大哥,确实厉害。
学霸君:除此之外,还有九个常用的积分公式


小e:哈哈哈,那么∫e^(-x^2)不定积分,我们就不怕了不定积分军了,传令兵,通知
全军集合,准备团战!!!

下期预告
厮杀的战场,孤寂的古城,仗剑走过的天涯,不过是所谓的南柯一梦。
下期,新人来访,小e迎来被辞退的危机,看似一场争锋相对的会议,究竟该如何收场?!?!

想要了解更多的高数知识么?
想要知道故事的后续发展么?
长按下方
关注河工大信越团!
下次高数我们不见不散!
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,加站长微信免费获取积分,会员只需38元,全站资源免费下载 点击查看详情
站 长 微 信: thumbxmw

