置信区间估计也是参数估计的一种,是用一个区间来估计参数值,confidence interval 也就是一定信心下的区间,如95%的置信区间为(0.76置信区间,0.96),就意味着有95%的信心认为(0.76,0.96)这个区间包含了总体参数。
在实际情况下,我们不可能做很多次抽样,也不可能计算很多个置信区间,绝大多数情况下,我们只能计算1个置信区间,由于总体参数是固定的,所以确切的描述是区间包含参数,而不是参数落在该区间。
置信区间与P值的关系
置信区间在作出统计学结论时与P值之间常常有异曲同工之妙,例如对于参数=0的无效假设,如果P值小于0.05,那么计算的该参数估计值的95%的置信区间一定不包含0,反之,如果P值大于0.05,那么计算的该参数估计值的95%置信区间一定包含0。

置信区间可以提供比P值更多的信息,如与无效假设的参数偏离有多远置信区间,如无效假设为两组收缩压的差值为0,最后计算95%置信区间为(0.1,0.15),这至少提示两点,首先两组差异有统计学意义,因为置信区间没有包含0,第二,两组总体的差值不大,因为我们有95%的信心认为两组差值在0.1~0.15之间,这说明尽管结果有统计学意义,但从专业角度来看,收缩压差别太少,没有太大的实际价值,这一信息是P值无法提供的。
利用标准误计算置信区间
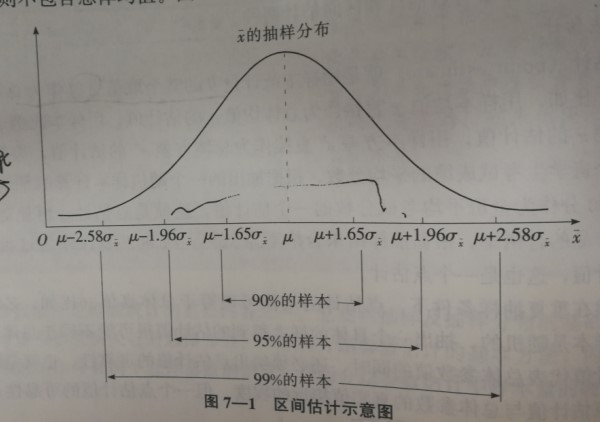
标准误是样本统计量的标准差,它反映了每次抽样样本之间的差异,如果标准误小,则说明多次重复抽样得到的统计量差别不大。
标准误和标准差之间具有一定的差异,前者是一种误差,而后者则是对均数的偏离,此外标准差是一个描述性指标,只是描述原始数据的波动情况,而标准误则是跟统计推断有关的指标,描述性指标和统计推断指标根本不是一个层次上的概念。最后他们针对计算的对象不同,标准差是根据某些抽样的原始数据计算的,而标准误是根据多次抽样的样本统计量(均数、率)来计算的。

关于均数和率的置信区间的计算公式详见本书P92。
Bootstrap法计算置信区间
Bootstrap法几乎可以用于计算各种参数的置信区间,无论其是否服从正态分布。该方法是利用重复抽样的方法对参数进行估计的,通过重复抽样计算得到每个样本的统计量,随后就可以根据这些统计量计算置信区间,而置信区间的计算又主要用百分位数法,其思想是计算出所有样本统计量的第2.5百分位数和第97.5百分位数,将其作为95%置信区间。但在估计结果有偏的情况下,就需要借助其他方法了,如本书P94中提到的百分位数t法。
Ref:《白话统计》 冯国双著
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,永久会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: thumbxmw

