今天是国际数学日,祝所有数学教师和数学教育研究者节日快乐!在这个属于数学的日子里,分享我们对小学数学教育的一些思考。
《圆柱的表面积》给我们的启示
王建明陈妍 韩天硕
在教师培训和教学研究中,我们经常要面对一线教师的各种课堂现象,作为教师培训者,如何观察到更多有意义的现象,给一线教师提出更多有意义的话题,这是非常有意思和非常要紧的事情. 下面我们给大家分享由北京市海淀区东北旺中心小学韩天硕老师执教的常规小学数学课《圆柱的表面积》中的一些现象,并给出进一步思考的问题.
一、主要活动
本节课主要活动有:
第一,认识圆柱的侧面。通过估算一个圆柱形薯片筒至少需要多少平方厘米的纸?(不包括重叠部分),探究圆柱的侧面展开图的形状.
第二,对学生给出的几种方法进行讨论. 学生得到侧面面积的大致方法有:(1)A4纸将圆柱围起来,随后将A4纸打开得到一个长方形;(2)将薯片筒的侧面剪开摊开得到了一个长方形,这个长方形就是圆柱的侧面积;(3)想象圆柱侧面展开图是一个长方形,用线绕圆柱一周,得到圆柱底面的周长(长方形的长),进而得到圆柱侧面积;(4)将圆柱的侧面剪开摊开成平行四面形,它的面积就是圆柱的侧面积.
第三圆台侧面积公式,计算薯片圆柱筒的表面积,得到圆柱的表面积的一般公式.
第四,运用公式.
毫无疑问,在上面所有活动中,第二个活动是关键,包括学生的空间想象力圆台侧面积公式,计算求解能力和逻辑推理能力的综合运用.
二、圆柱与圆锥的统一认识
我们知道,圆柱和圆锥都是特殊的柱面和锥面,它们的准线均为圆.
1. 什么是柱面和锥面
柱面的定义:三维欧氏空间中,动直线沿一条定曲线平行移动所形成的曲面叫做柱面. 定直线叫做该柱面的准线,平行直线叫做该柱面的母线.
当准线为一个定圆时,叫做圆柱面. 特别地,当定圆所在平面与母线垂直时,叫做直圆柱面或正圆柱面. 小学数学和中学数学中,往往研究的是正圆柱面(简称圆柱),圆柱往往是有上下底面的,即此时圆柱是有侧面和底面的.
正圆柱面也可以看成是与定直线平行的动直线绕定直线旋转一周而形成的曲面. 这也就是小学课程里面讲的圆柱,即圆柱是一个长方形绕它的一条边旋转一周所得到的封闭图形.
锥面的定义:三维欧氏空间中,过一个定点的动直线沿一定曲线移动所形成的曲面叫做锥面. 定点叫做该锥面的顶点,定曲面叫做该锥面的准线,动直线叫做该锥面的母线.
当准线为一个定圆时,叫做圆锥面. 特别地,当定圆所在平面与母线垂直时,叫做直圆锥面或正圆锥面. 小学数学和中学数学中,往往研究的是正圆锥面(简称圆锥),圆锥往往是有下底面的,即此时圆锥是有侧面和底面的.
正圆锥面也可以看成是与定直线有公共点的动直线绕定直线旋转一周而形成的曲面. 这也就是小学课程里面讲的圆锥,即圆锥是一个直角三角形绕它的一条直角边旋转一周所得到的封闭图形.
在小学数学课程中,没有圆锥的侧面的学习,应该是考虑到侧面的空间想象能力要求较高和扇形面积不易掌握.
事实上,即使不讲圆锥侧面面积的计算公式,但可以把圆柱和圆锥的侧面展开图放在一起研究,通过操作,学生可以理解圆柱和圆锥侧面展开图分别是长方形和扇形.
2. 圆柱与圆锥的统一性认识
之一:圆柱和圆锥是运动过程中的两种特殊位置.
如图1所示,ABCD为直角四边形,绕直角边AB旋转一周,得到一个正圆台.
当CD⊥AD时,得到一个圆柱(如图3);
当B与C重合时,得到一个圆锥(如图2);

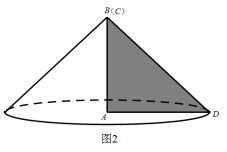
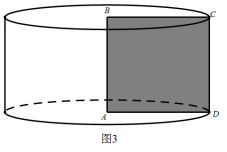
圆台在小学可以略去,小学里的圆柱和圆锥实际上是圆台的两个极端情况,有了运动的观点看问题,圆柱和圆锥就可以统一在一起认识和研究.
之二:圆柱和圆锥的侧面都是可展曲面.
圆柱和圆锥的侧面展开图分别是长方形和扇形,它们都是扇形环的特殊情况. 圆台的侧面展开图是扇形环.
直观上看,圆柱和圆锥(圆台又可以看成是圆锥切掉了一个小圆锥剩下的几何体)的侧面都可展开为平面的一部分,这样的曲面叫做可展曲面.
事实上,在三维欧氏空间中,柱面和锥面是主要的两类可展曲面,后面可以数学上看到三维欧氏空间中,可展曲面一共就只有三类.
3. 什么是可展曲面
进一步的问题是“什么是可展曲面”. 考虑到本文主要的阅读对象是小学数学教师,我们只从直观上解释.
我们知道曲面有很多种情况,比如球面、柱面、锥面、双曲抛物面(马鞍面—薯片)、单叶双曲面(广州电视塔—小蛮腰,首钢冷却塔)、悬链面等等.



有的曲面上没有直线,有的曲面上有直线,如果一个曲面可以看成是由直线在空间中的运动生成的,这样的曲面叫做直纹面.比如圆柱面和圆锥面都是直纹面,而球面不是直纹面,悬链面也不是直纹面.
有些曲面初看起来表面的确是弯曲的,比如双曲抛物面(马鞍面)和单叶双曲面,但事实上它们是由直线运动而生成的曲面.正是由于这些曲面是直纹面,所以在建筑美学中被广泛使用.
在直纹面中,还有一类曲面,它在局部可以与平面保持等距变换,在不拉伸、收缩、不皱褶或撕裂的情况下局部可弯曲为平面的一部分.直观上就是把曲面沿直线剪开,再摊平就是平面的一部分,这样的直纹面叫做可展曲面.
4. 可展曲面的分类与判定
关于直纹面和可展曲面的严格数学公式定义,有兴趣的读者可以参考几乎任何的《微分几何》教材. 下面给出可展曲面的几个定理.
定理1:可展曲面的高斯曲率等于零;反正亦然.
定理2:两个等常高斯曲率的曲面之间存在等距变换.
定理3:平面的高斯曲率等于零.
定理4:在三维欧氏空间中,可展曲面只有三类:柱面、锥面和空间曲线的切线曲面.
三、圆柱螺旋线的数学含义
我们注意到本节课中还有一个环节——把侧面剪开摊开得到一个平行四边形,后来与执教教师询问知道他们是受卫生纸的圆筒上纸痕得到的启发. 为什么可以剪开摊开得到平行四边形?

数学原理:平行四边形的斜边在圆柱面上是圆柱螺旋线.
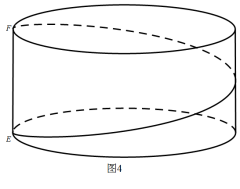
一方面,事实上,圆柱面上的“直线”不仅有直母线,还有圆柱螺旋线. 也就是说,我们需要回答“给定圆柱面上两个定点,经过这两点的最短路径有哪些曲线?”.
(1)如果给定的两点是直母线的两点,经过这两点的最短路径是直母线.
(2)如果给定的两点在一个圆上,经过这两点的最短路径是这个圆所在曲线.
(3)如果给定的两点是其他情况,经过这两点的最短路径是过这两点的圆柱螺旋线.
要数学地证明上述命题,就涉及到更多的数学概念,特别是“直线”的本质意义. 一般而言,曲面的测地曲率为零的曲线是所谓最短路径,数学上把这样的曲线叫做测地线(测地线是直线概念的推广,比如球面上的测地线是大圆—即球面上的“直线”是大圆).
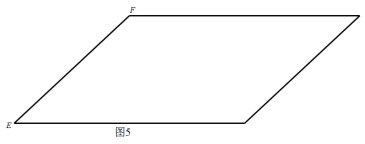
另一方面,可以反过来认识. 一个平行四边形也可以卷成与圆柱一样的曲面,边EF在圆柱侧面上就形成一条圆柱螺旋线.
或者,连结给定长方形的对角线,再把该长方形卷成一个圆柱,那么对角线留在圆柱侧面上的痕迹就是一条圆柱螺旋线.
圆柱螺旋线的几何意义:空间中动点在水平面上做均速圆周运动的同时,在竖直方向上做均速直线运动,动点的轨迹叫做圆柱螺旋线.
这样就解释了本节课中的平行四边形活动合理性,但是学生可能很难想到平行四边形展开的方法.
四、小学课程里圆柱表面的其他问题
1. 圆柱(圆锥)侧面上有给定的两点A,B,一只蚂蚁沿什么路径从A到B,所走的路径最短?
这个问题的回答,实际上就与前面的分析有关. 要看两点A,B在圆柱(圆锥)面上的分布情况而具体分析. 如果有一点在圆柱(圆锥)底面,情况会更复杂一些,但分析思路与前文一致.
2. 小学里的正方体和长方体显然也是可以展开为平面图形的,那么它们是不是柱面或锥面?
长方体和正方体都是柱面的特殊情况,只是在一般柱面上加了上下底面而已. 长方体和正方体作为柱面,它们的准线是长方形或正方形(平面多边形). 因此,简单多面体可以看成是柱面或锥面加了上(下)底面. 这些立体图形可以展开成平面图形的数学原理与一般柱面或锥面是可展曲面的数学原理是一致的.
3. 生活中圆柱形外包装的侧面多是近似正方形吗?
本节课中,教师提供的薯片筒的外包装展开图近似于正方形,这也造成很多学生在后面的描述时,以为圆柱的侧面展开图总是正方形. 由此,我们提供一个综合实践的教学资源框架:超市中常见的圆柱形外包装的展开图的长宽比是什么分布?
后记
以上是我们在一节常规小学数学课后的思考与建议. 数学教育是科学与艺术的结合. 事实上,如何策略地组织学生的学习,如何艺术地组织教师的“教”,这些话题还是像吴正宪、华应龙这样的小学数学教育家和广大的一线小学数学教师更有发言权,我们的分析与建议更多地是从学科本体和科学原理上提供一些可能的视角.
文章预告:
一道初三平面几何题的哲学反思
说不尽的三角情结
往期文章:
微信公众号推送算法的改变,点个“在看”哟
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,加站长微信免费获取积分,会员只需38元,全站资源免费下载 点击查看详情
站 长 微 信: thumbxmw

