本篇推送由以下作者合力完成
G1710蒋凌睿 G1710张思源
前言
众所周知,数学一轮复习会把高考要考的知识点完完整整地过一遍——相当于是用几个月的时间再上一遍高一高二的课。不过有了高一高二的知识储备,大家进行一轮复习的速度会比较快。如果按六道大题的版块梳理的话,在期中之前大家会复习完三角函数、数列、导数的基本知识,而在期末之前统计与概率、立体几何和解析几何也会结束。接下来本文将从不同维度给予大家一些复习建议,希望能对大家的学习有所帮助。
01
知识点总结
02
技巧归纳
03
方法
04
常见误区
1
知识点
1.三角
高考涉及到的三角题有两种:三角函数和解斜三角形,which你们在期中考试中应该都会遇到。如果考三角函数,那么可能会考到诱导公式、和差角公式、二倍角公式、升降幂公式和辅助角公式。如果考解三角形,那么可能会考正弦定理、余弦定理。
2.数列
这是最简单的一部分超几何分布的期望和方差公式推导,因为高考数列不会考递推方法,基本上只考等差数列、等比数列,所以只要掌握好等差、等比数列的通项公式和求和方法就就可以啦。
3.立体几何
立体几何一般会有2~3问。第一问是纯几何证明,需要你掌握线线、线面、面面的垂直和平行关系的性质定理和证明方法。(这3*2=6种待证结论我还真都在题目中见过。)这些证明过程都很容易漏写一些关键条件,所以老师大多都会建议大家去背一背这些结论都是几推一。不过如果有比较好的几何直观,这些不背也罢。
第二问和第三问一般是线线角、线面角和面面角的计算超几何分布的期望和方差公式推导,你需要掌握空间直角坐标系、法向量及其夹角的运算,以及把空间角问题转化为法向量夹角问题的方法。
4.统计与概率
一般来说统计与概率第一问会考古典概型、用频率估计概率、简单随机抽样和分层抽样等等,第二问会是分布列和数学期望,考察分布列和数学期望的概念、组合计数与古典概型,第三问会是开放性问题,需要综合前面说过的知识点解答。
5.平面解析几何
这部分需要你掌握平面直角坐标系内直线、圆锥曲线的方程、圆锥曲线的离心率(就是个概念空壳,因为圆锥曲线的第二定义被砍了)、向量的数量积的坐标表示、两点间距离公式(请注意,高考中弦长公式不能直接用)、点到直线距离公式、直线和圆的位置关系、直线与二次曲线的位置关系、两圆之间的位置关系。
6.导数

课改以后砍掉了复合函数求导(别不信,2020年北京高考的导数题甚至连求导都不用),所以导数只需要掌握初等函数的导数、导数的四则运算、运用导数求切线方程、运用导数的符号判断原函数的单调性即可。
7.压轴题
这部分呢,可以说没有基础知识,也可以说有很多很多基础知识。而且此类题目的做题技巧非常重要,重要性显著高于硬性的知识。如果有机会的话我们会推出一个专题专门讨论北京高考数学的压轴题,此处先略去不提。
以上这些拥有姓名的知识都是基础中的基础。如果对它们还有困惑的话,一定要在一轮复习中解决掉,否则请准备好在期中考试过后面对数学老师的冷嘲热讽。
2
技巧
对于任何一份数学卷子,都由三部分组成:选择、填空、解答,其中每一个部分除最后一道题外都一定可以用课内讲过的方法解决,那么考生要做的事就可以划分为两个部分:用尽一切办法把常规题搞定,把最后一道题解出来/混到分。
选择填空最后一题老师会发一本专门的习题册练习,凭借经验即使是数学的差生全部做完也都十拿九稳了。大方向包括硬算,特殊值,大胆猜想等方法,重要的是通过做题找到感觉。没有固定的方法。
其次是解答题,一般包括数列/三角,立体几何,概率,解析,求导,压轴题。按照常理来说顺序应该如此,但今年高考前两道题换了个位置,不过这两道题都属于简单题,无论顺序如何变难度与做法几乎是不会变的。解析求导两道题可以互换位置。
数列题一般是等差,等比,或二者结合。如果第一问是给出已知等差/等比,以及若干条件,那就直接设出来未知数(a1,q,d等等)然后按照题意列方程,给结果(解的过程可以忽略),最好检验一下解是符合题意的,再把数列表达出来即可。另一种题型是给出条件,你需要证明等差/等比的,一般用到的是定义,把已知式变化为两项相减或相除,但再强调一遍,证明的最后一步一定要回到定义。式子如果比较复杂可以先把前几项带进去找到规律,再通过规律反推出变形方式。即使真的算不出来,也不要浪费太多的时间,可以采用第一或第二数学归纳法进行证明(强烈建议把归纳法的步骤和规范过程练好,在最后一道题也会有帮助)。第二问是建立在第一问的基础上计算某个数列的前n项和,或证明一个相关的不等式。前者的话,只需等差、等比、错位相减法便足够了,后一个需要一定的放缩技巧,平时需要一定的积累。
三角题包括三角函数和解斜三角形。三角函数只需要基本功足够扎实+过程规范即可,不需要过多赘述。关于解斜三角形,有一个不成文的规定,正弦定理和余弦定理都会用到且不会重复,故假如第一问正弦定理用的很舒服,那第二问大概率就是余弦定理能解决的问题了。另外虽然题目已经规定了三角形,但由余弦值或正弦值到角的大小时还是要有掐角的这一步的。海伦公式是一个不错的技巧,即使不能直接用也可以作为检验的手段,建议大家掌握。
立体几何,纯套路题,把线、面有关的几推几掌握好了第一问信手拈来。辅助线的话一般看到中点与中位线有关,矩形的平行关系也一定会有用的。(曾经遇到过一道很难的题垂直关系是由勾股定理得出来的,大家做题时需要留心,如果垂直平行关系题干给的不够多,而数字非常奇怪,那就有可能需要走这条路了。)第二三问(如果有的话)就需要建立空间直角坐标系,一定要把三组垂直清晰地摆出来,并在图上标明正方向,采用右手系。最后如果求二面角余弦值需要区分钝角和锐角,一定要把角度范围写出来再给值。如果一眼看不出来,就在法向量上做功夫:一个指向二面角内,一个指向二面角外,单位向量点乘得到的余弦值就是真正的二面角余弦值了。
概率,简单题但却是很多尖子生最头疼的题,技巧就是多写!基本事件空间要设,题干中没出现的数字怎么来的要说明,事件要设,由部分估计整体还是由频率估计概率想清楚,最好求出答案后再写个解把问题回答了,第一问妥妥的满分。第二问常规情况是求数学期望,各种情况求出概率后先不要上下消掉公因数,把他们加起来看看是不是1,检验一下再消掉。求数学期望要按照定义求,但结果也要检验一下(二项分布,超几何分布都是有简单公式的,建议把期望公式和方差公式背下来)。非常规题目(比如今年高考题)是要求一个复杂事件的概率,用常规方法先做一遍,然后求反面概率检查一下。第三问可能是比较两种情况的方差,期望等的大小,这种题目不需要给出过程,硬算可以出来结果,也可以举一个特殊例子。另外就是用数据说话,这种题目没有唯一标答,大家不要被数学的严谨性束缚,用平均数,众数,增长量往你的论点上靠就行,但千万不要只说“趋势”二字,一定要有数据支撑。

解析题目我们这一届不会考双曲线了,就论椭圆和抛物线。第一问设未知量,把题干信息转化为方程,解出来即可,千万不要求错,最好立刻检查一遍(哪个是长轴,以及抛物线开口方向 )。第二问要设点或设线,如果题目给出来设的目标就不要再另起炉灶了,如果没给就需要自己斟酌,但设线的情况比较多,可以优先考虑。解析几何思路不难,就是麻烦,思绪不能乱。联立,求点,韦达定理,目标式证明一步步来,千万不要慌了忘记中心未知数是谁。另外,同理可得的式子不用再求一遍了(比如一个斜率是k,一个是1/k,算完第一个之后直接把k=1/k带进去就可以得到第二个式子)。抛物线的话还要记得点到焦点距离等于点到准线距离。最关键的是一定要把计算能力提上来,这是学好解析几何的必要条件。
举个例子
(据说这是高考解析几何的天花板,方法不一定最简单,但思路应该是很清晰的)


导数题首先是要把函数求出来(比如今年高考,但一般不需要),然后有四条路径:参变分离,变形成简单式,直接解,其他(比如某个函数最大值小于另一个函数的最小值等等,很少见),所有的方法一定是课内讲过的,一定要把当时没想到的方法记下来,这比做多少道相同类型的导数题都管用。另外,需要掌握一定的放缩技巧,对掐点或者将题目简化很有利,比较常用的詹森不等式。另外如果时间充沛,还要掌握无论什么方法都有思路算下去的能力(把一个大问题拆解成多个讨论的小问题,分布解决。或者求三到四阶导也不要慌。无论做法是什么只要是对的都会给满分的),举一个爆算解导数的例子(标准做法就不展示了)


3
方法
数学作为经典理科是典型的思路大于做题大于死记硬背的。就拿立体几何的几推几来说,其实完全没有背的必要,每次推导时就在脑海中构建一个空间。比如面面垂推导线面垂,“平面α⊥平面β”就把任意位置关系的两平面局限在垂直平面了。“直线l在平面α上”就在平面上想一条线,但这个线是随意的。“l垂直于交线m”这样l的方向也就锁定了,最后只需要“平面α∩平面β=m”把交线定义出来即可。如此方法所有立体几何的推导都不需要死记硬背了。
所有数学公式都是推导出来的,理论上你不需要背任何东西。另一方面,背知识点可以加快做题速度。所以什么要背什么不用背现场推就很关键,每个人喜好不同但一定要有这个意识,不要所有东西都背,否则会学的很累,而且会让数学丧失美感。我个人的话必须要背的有:立体几何各种体的定义、求导公式(尤其是指数函数和幂函数)、合角公式(差角,二倍角,半角等等都可以从这个推出来)等
不用背但推导很方便的:各种函数的图像随参数变化的变化,概率方面的公式等
平时需要总结的:基本的缩放,二级结论,最好可以看看高联教材中简单的与高考有关的公式,最后一题的做法(大方向)
关于用在数学上的时间(选择性接受):一般的数学题不用刻意刷,上课时老师会发卷子或布置题,那些量就足够了。说一些数学老师不爱听但确实可以提高效率的话,题如果会做的话且用的是正常方法,老师讲课时其实不用听讲。自己想到的是特殊技巧方法等老师讲的时候看看老师的思路自己知不知道,知道的话继续干自己的事,不知道的话尝试理解并记忆。如果自己的方法很笨,恭喜你在考场上没思路时做出题的概率又增加了,但也一定要听老师讲正经方法。总结就是,用正常方法做出来不用听特殊方法,用特殊方法做出来一定要再用正常方法做一遍。
做理科题目我是推荐做完几道题立刻对答案的,因为这时候自己的思路还在,还可以通过对比发现自己的问题。而一旦隔了一天再看,只会知道什么是正确思路,却无法修正自己的错误思路,下次可能还会走入同样的死路。而且理科题做完了答案对完了想通了就不需要额外的事情做了,适合在学校完成,尽量不要拖到回家做,家庭作业时间还是留给语文和英语这种需要思维量的学科吧。(课间或者其他课上不用听的时间把数学做一做,基本上发的卷子两节课内就能刷完)数学不需要专门抽时间来准备,每天刷完学校的题,听一下老师的思路,修正自己的思路,继续刷剩下的题就足够了。
4
一轮复习常见误区
1.不要现在就开始研究如何骗分
虽然骗分能让你从80分提升到110分,但绝不可能让你从110分提升到140分。一轮复习还是应该以知识的积累和能力水平的提升为第一要务,当你的水平到达了一定的高度后,你就不需要再去骗分了,而如果达不到,你用最后一个月的时间去研究如何骗分也是来得及的。在一轮复习就去研究如何骗分只会让你陷入一个舒适区,让你安于难题能得一半左右分数的现状而不去思考如何把难题做出来,显然是不利于你进一步的提升的。
2.重视基础≠重视概念
一轮复习强调重视基础,但重视基础并不是重视概念。像什么复数的虚部是实数、(x+y)n的展开式中yn是第n+1项之类无聊的事情有点印象就行了。重视基础意味着对于书上的工具、定理和方法的准确理解。高考题不会让你默写复数的虚部的概念(那是文科的考法),但是下面这题你对导数和单调性的关系理解得稍有偏差就会做错:
已知f(x)在R上可导,则“f(x)单增”是“f(x)≥0恒成立且不存在或只存在有限多个x∈R使得f'(x)=0”的
A 必要不充分条件
B 充分不必要条件
C 充要条件
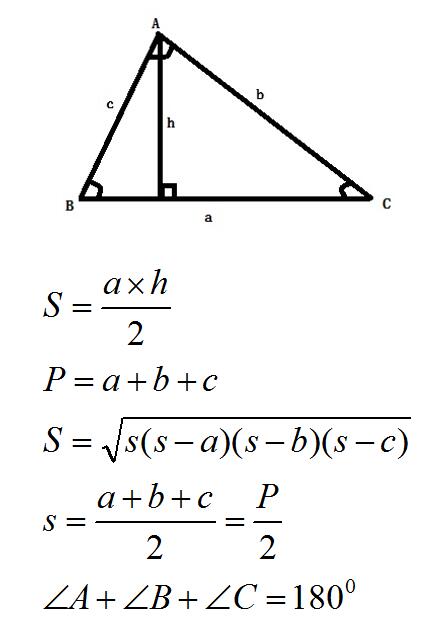
D 既不充分也不必要条件
3.你不需要会≠你会了没用
自从教材改革以后书上很多东西都被砍了。所以在一轮复习中这些内容也就被很多同学忽略了。但是请注意,它被砍了并不代表你不能会,更不代表你会了以后就用不到。事实上,这些超纲的内容有时可以为你提供某些题目的第二种做法,让你检查出一些不该犯的错误。
就以2020年北京高考为例,第9题你可以用和差化积验证,第10题可以用小量近似验证,第19题可以对分子用多元均值,第20题用射影几何的结论很容易证明AP,AQ;AB,A∞是调和线束(从而该比值为1)。这些题目也都是丢分的重灾区,而用这些超纲的方法给予检验可以在很大程度上避免计算错误,所以在一轮复习中关注一下这些超纲知识还是非常有必要的。
4.不要急于大量刷题
现在还只是一轮复习,主要任务是搞懂基础知识,掌握基本的技巧,而往年的题应该在你对基础知识已经有了比较好的掌握以后再刷。一是因为现在如果你现在没有构建一个比较完整的知识体系的话,刷题的意义不大,而且还会浪费一些好题;二是因为某些区县的题目只有通过一些奇技淫巧才能做出来,(某区期末和某区二模竟不约而同地考了阿贝尔和式变换,给我看傻了。)现在就刷容易带偏你的复习轨迹。等到二、三轮复习时再刷题也不迟。
结语
数学学科讲究的更多是思维和从题目信息分析切入点的能力,而不是一味地死记硬背。做明白一类题,深度理解一种方法,远比做完一套题有用。接下来如果有机会我们也会作出更多分享,希望能有所帮助。
编辑 | 赵云笛
文字 | 蒋凌睿 张思源
欢迎关注水母行动:)
—如果有问题或者想加入/供稿欢迎后台联系—
水母君期待认识可爱的你哟!
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,加站长微信免费获取积分,会员只需38元,全站资源免费下载 点击查看详情
站 长 微 信: thumbxmw

