考点2 集合的基本运算
【基础回顾】

一、课本基础提炼
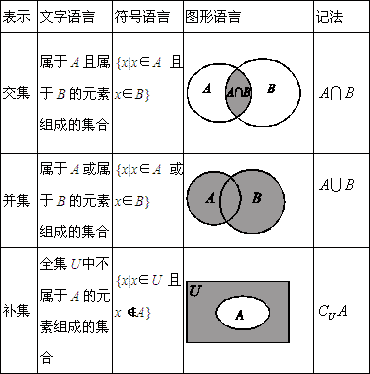
1.集合的基本运算:交集、并集、补集.
二、二级结论必备
1.常用集合关系的结论:
(1)
(2)
(3)CU(A∪B)=(CUA)∩(CUB);CU(A∩B)=(CUA)∪(CUB)
【技能方法】
1.并集、交集、补集的简单运算:
集合的运算中要根据集合的定义把参与运算的各个集合求出,再根据交、并、补的定义进行运算.此类题目首先应看清集合中的元素的范围,简化集合,若是用列举法表示的数集,可以根据交集、并集、补集的定义直接观察或用 图表示集合运算的结果;若是用描述法表示的数集,可以借助数轴分析写出结果,此时要注意当端点不再集合中时,应该用“空心圈”表示.
例1 (1)若集合A={2,4,6,7},B={3,4,5,7},则A∩B=____.
(2)集合
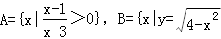
则A∩B=_____,A∪B=______,(CRA)∩B=______.
【答案】(1){4,7};(2)A∩B={x|1<x≤2},
A∪B={x|x<-3或x≥-2},(CRA)∩B={x|-2≤x≤1}.
【解析】
(1)A、B的共同元素为4、7,所以A∩B={4,7}.
(2)因为A={x|(x-1)(x+3)>0}={x|x<-3或x>1}
B={x|4-x2≥0}={x|-2≤x≤2}在数轴上画出A、B,

所以,A∩B={x|1<x≤2},A∪B={x|x<-3或x≥-2},
(CRA)∩B={x|-2≤x≤1}.
【点评】集合的运算中要根据集合的定义把参与运算的各个集合求出,再利用数轴,根据交、并、补的定义进行运算.
2.已知集合的交并集求参数的取值范围
依据数形结合的数学思想,利用数轴分析法是解决有关集合交集、并集问题,特别是一些字母范围问题的常用方法.
例2 已知A={x|2a≤x≤a+3},B={x|x<-1或x>5},若
,求a的取值范围.
【解析】
由
(1)若
,有2a>2+3,所以a>3.
(2)若
,如下图:
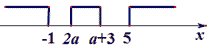

综上所述, 的取值范围是
【点评】
由
,则要考虑
两种情形,这样才不会漏解.
3.交并集性质的应用
在利用集合的交集、并集性质解题时,常常会遇到A∩B=A,A∪B=B等这类问题,解答时常借助于交、并集的定义以及集合间的关系去分析,如
,
例3设A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0}.
(1)若A∩B=B,求a的值.
(2)若A∪B=B,求a的值.
【解析】A={-4,0}.
(1)∵A∩B=B,∴
.
①若0∈B,则
.
当a=1时,B=A;当a=-1时,B={0};
②若-4∈B,则
当a=7时,B={-12,-4},
③若
.
由①②③得,a=1或a≤-1.
(2)∵A∪B=B,∴
∵A={-4,0},又因为B中最多只有两个元素,
∴A=B.
由(1)知a=1.
【点评】
要注意条件等价转化的运用,常见转化有
.
4.补集的思想的应用
对于一些比较复杂、抽象,条件和结论之间关系不明确,难于从正面入手的问题,在解答时,应及时调整思路,从问题的反面入手,探索已知与未知之间的关系,这时能化难为易,化隐为显,从而将问题解决.
例 4 若集合A={x|ax2+3x+2=0}中最多有一个元素,求实数a的取值范围.
【解析】
假设集合A中含有两个元素,即ax2+3x+2=0有两个不相等的实数根,则

,解得a<9/8且a≠0,则a的取值范围是{a|a<9/8且a≠0}.
在全集U=R中高一集合练习题,集合{a|a<9/8且a≠0}的补集是{a|a≥9/8或a=0}.
所以满足题意的a的取值范围是{a|a≥9/8或a=0}.
【点评】
集合A中的元素包含0个或1个,若采取分类讨论的策略,所分情况比较多,求解比较麻烦,构造其“补集”:集合A中含有两个元素,然后再求其补集,问题就得到了简化.
【基础达标】
1.【2015吉林三模】设全集U=N*,A={2,3,6,8,9},B={x|x>3,x∈N*},则图中阴影部分所表示的集合是()

A.{2}B.{2,3} C.{1,2,3}D.{6,8,9}
【答案】B
【解析】A∩B={6,8,9},所以图中阴影部分所表示的集合是{2,3},故选B.
2.【2015高考四川,理1】设集合A={x|(x+1)(x-2)<0},集合B={x|1<x<3},则A∪B=()
A.{x|-1<x<3}B.{x|-1<x<1}
C.{x|1<x<2} D.{x|2<x<3}
【答案】A
【解析】A={x|-1<x<2},B={x|1<x<3},∴A∪B={x|-1<x<3},故选A.
3.集合
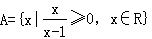
,B={y|y=2x+1,x∈R},则CR(A∩B)=()
A.(-∞,1]B. (-∞,1)C. (0,1]D. [0,1]
【答案】A
【解析】

B={y|y=2x+1,x∈R}=(1,+∞)
∴A∩B=(1,+∞),CR(A∩B)=(-∞,1],故选A.
4.已知集合A={x|x>1},B={x|x<m},且A∪B=R,那么m的值可以是()
A.-1B.0C.1 D.2
【答案】D
【解析】∵A∪B=R,A={x|x>1}∴B={x|x<m}要包含所有的小于等于1的实数,因此m>1,故选D.
5.若集合M={x|x2+x-6=0},N={x|ax-1=0},且N∪M=M,则实数a的值为________.
【答案】0或-1/3或1/2
【解析】
M={x|x2+x-6=0}={-3,2},由题意
当a=0时,
;
当a≠0时,N={1/a},要使
,则1/a=-3或2,解得a=-1/3或1/2.
综上所述,实数a的值是-1/3或1/2或0.
【能力提升】
1.【2015呼伦贝尔二模】已知
,A={y|y=sinθ,θ∈R},则P∩Q=()
A.
B.{0}C.{-1,0}D.
【答案】C
【解析】
,Q={y|y=sinθ,θ∈R},
所以Q={y|-1≦y≦1},所以P∩Q={-1,0},故选C.
2.【2015济南市高三上学期期末】已知集合M+{x|x2-4x<0},N={x|m<x<5},若M∩N={x|3<x<n},则m+n等于()
A.9B.8C.7D.6
【答案】C
【解析】M={x|x2-4x<0}=(0,4),N=(m,5),
若M∩N=(3,n),则
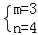
则m+n=7,故选C.
3.设集合A={x|a-2<x<a+2},B={x|x2-4x-5<0},若
,则实数a的取值范围为()
A.[1,3]B.(1,3)C.[-3,-1]D.(-3,-1)
【答案】A

【解析】
B={x|x2-4x-5<0}={x|-1<x<5},因为
,所以
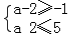
,解得:

,所以实数a的取值范围是[1,3],故选A.
4.已知集合A={-1,1,3},B={1,a2-2a},A∩B=B,则实数a的不同取值个数为()
A.2 B.3 C.4 D.5
【答案】B
【解析】
由题意
,所以a2-2a=-1或a2-2a=3,解得:a=1或a=-1或a=3,所以实数a的不同取值个数为3,故选B.
5.已知
,N={(x,y)|ax+2y+a=0}且
则a()
A.-6或-2B.-6C.2或-6D.-2
【答案】A
【解析】
集合M表示去掉一点A(2,3)的直线3x-y-3=0,集合N表示恒过定点B(-1,0)的直线ax+2y+a=0,因为
,所以两直线要么平行,要么直线ax+2y+a=0过点A(2,3).因此
或2a+6+a=0,即a=-6或-2,故选A.
【终极突破】
1.设常数a∈R,集合A={x|(x-1)(x-a)≥0}
B={x|x≥a-1},若A∪B=R,则a的取值范围为()
A.(-∞,2)B. (-∞,2]C.(2,+∞)D. [2,+8)
【答案】B
【解析】集合A讨论后利用数轴可知,
,解得a≤2,所以 的取值范围是(-∞,2],故选B.
2.集合A={x|x2+2x-3>0},B={x|x2-2ax-1≤0,a>0}.
若A∩B中恰含有一个整数u,则实数a的取值范围是()
A.(0,3/4)B.[3/4,4/3)
C.[3/4,+∞)D.(1.+∞)
【答案】B
【解析】
由A={x|x2+2x-3>0}可得A={x|x<-3或x>1} .由x2-2ax-1≤0,a>0,解得x1≤x≤x2.由韦达定理可得x1<0,x2>0.根据题意A∩B中恰含有一个整数u,所以
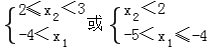
(舍去,由于a与
很接近).即
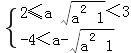
,解得3/4≤a<4/3,所以实数a的取值范围是[3/4,4/3),故选B.
3.集合A={(x,y)||x|+|y|≤1},B={(x,y)|(y-x)(y+x)≤0},集合M=A∩B,若动点P(x,y),则x2+(y-1)2的取值范围是()
A.

B.
C.
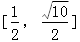
D.
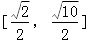
【答案】A
【解析】
集合M=A∩B表示平面内由点(0,0),
,(-1,0),

构成的正方形与点(0,0),
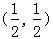
,(1,0),
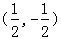
围成的正方形,x2+(y-1)2看作点(x,y)、(0,1)距离的平方高一集合练习题,结合坐标系可知x2+(y-1)2的取值范围是
,故选A.
4.已知集合U={(x,y)|x∈R,y∈R},M={(x,y)||x|+|y|<a},
P={(x,y)|y=f(x)},现给出下列函数:①y=x-a;
②y=㏒ax;③y=sin(x+a);④y=cosax.若0<a<1时,恒有P∩CUM=P,则所有满足条件的函数f(x)的编号是____.
【答案】①②④.
【解析】依题U={(x,y)|x∈R,y∈R}表示整个平面直角坐标系区域,M={(x,y)||x|+|y|<a}表示如图所示的平面区域,p={(x,y)|y=f(x)}表示平面直角坐标系上函数y=f(x)的曲线,
若0<a<1时,恒有P∩CUM=P,则P与M无公共点,依题可知①②④函数的曲线与M均无公共点,对于③,当x=0时,y=sina,又因为sina<a,所以y=sin(x+a)曲线上的点(0,sina)必定在M表示的平面区域内,即P∩CUM≠P,故应填入①②④.
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,加站长微信免费获取积分,会员只需38元,全站资源免费下载 点击查看详情
站 长 微 信: thumbxmw

